10-3　タイムマネジメント

令和6年6月修了試験　 問42

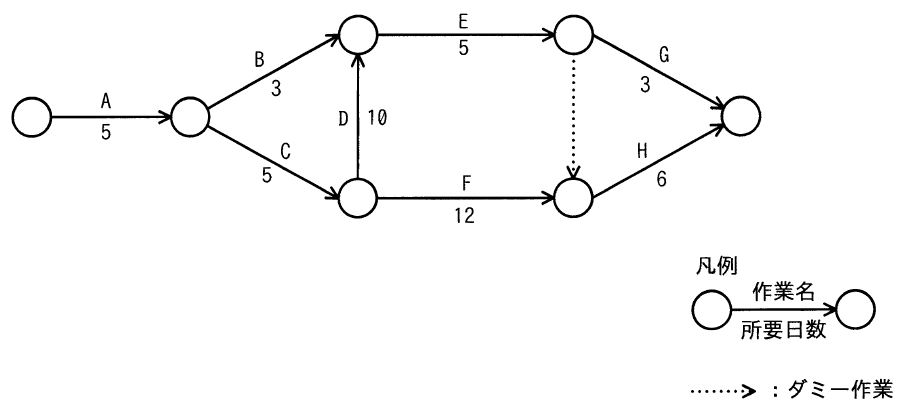
アローダイアグラムで表される作業A～Hを見直したところ,作業Dだけが短縮可能であり,その所要日数は6日に短縮できることが分かった。作業全体の所要日数は何日短縮できるか。

解答　ウ

【頭の準備体操】
クリティカルパスは，全ての経路の中で最も日数を要する経路。

A → B → E → G：5＋3＋5＋3＝16日
A → B → E → ダミー → H：5＋3＋5＋0＋6＝19日
A → C → D → E → G：5＋5＋10＋5＋3＝28日
A → C → D → E → ダミー → H：5＋5＋10＋5＋0＋6＝31日(クリティカルパス)
A → C → F → H：5＋5＋12＋6＝28日

作業Dを6日短縮すると，
A → B → E → G：16日
A → B → E → ダミー → H：19日
A → C → D → E → G：5＋5＋6＋5＋3＝24日
A → C → D → E → ダミー → H：5＋5＋6＋5＋0＋6＝27日
A → C → F → H：28日(クリティカルパス)

よって，作業全体の所要日数は，31日から28日の3日短縮できる。

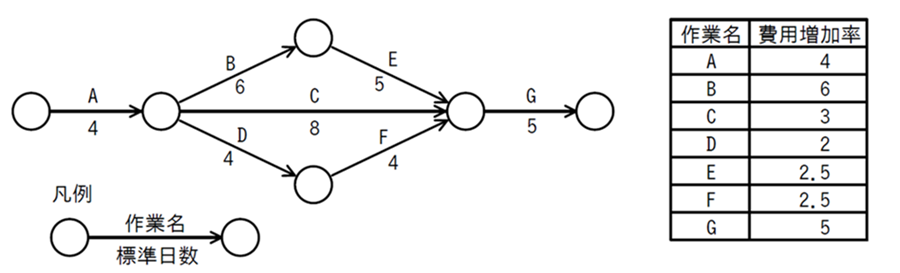
令和5年度公開　 問13

図に示すとおりに作業を実施する予定であったが,作業Aで1日の遅れが生じた。各作業の費用増加率を表の値とするとき,当初の予定日数で終了するために掛かる増加費用を最も少なくするには,どの作業を短縮すべきか。ここで,費用増加率とは,作業を1日短縮するために要する増加費用のことである。

解答　エ

【頭の準備体操】
クリティカルパスは，全ての経路の中で最も日数を要する経路。
クリティカルパス上の作業が遅れると，プロジェクト全体の遅れにつながる。

A → B → E → G：4＋6＋5＋5＝20日(クリティカルパス)
A → C → G：4＋8＋5＝17日
A → D → F → G：4＋4＋4＋5＝17日

作業Aはクリティカルパス上にある。
当初の予定日数で終了するためには，クリティカルパス上の作業A以外の作業B，作業E，作業Gのいずれかを1日短縮する。

ここで，費用増加率をみると，
作業B：6
作業E：2.5(最も少ない)
作業G：5