基本情報技術者講座
★ 猫本 11-10 オペレーションズリサーチ(その3) ★
基本情報技術者 平成29年度秋期 問61
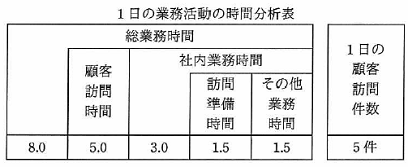
ある営業部員の1日の業務活動を分析した結果は,表のとおりである。営業支援システムの導入によって訪問準備時間が1件あたり0.1時間短縮できる。総業務時間と1件当たりの顧客訪問時間を変えずに,1日の顧客訪問件数を6件にするには,"その他業務時間"を何時間削減する必要があるか。
| ア | 0.3 |
| イ | 0.5 |
| ウ | 0.7 |
| エ | 1 |
解説
・1日の顧客訪問件数が5件の場合
総業務時間:8時間
1件当たりの顧客訪問時間:5.0時間÷5件=1.0時間
1件当たりの訪問準備時間:1.5時間÷5件=0.3時間
その他業務時間:1.5時間(顧客訪問とは関係がない)
・1日の顧客訪問件数が6件の場合
総業務時間:8時間(問題より時間は同じ)
1時間当たりの顧客訪問時間:1.0時間(1件当たりの顧客訪問時間は同じ)×6件=6.0時間
1件当たりの訪問準備期間:0.2時間(1件あたり0.1時間短縮)×6件=1.2時間
ここで,その他業務時間をxとする。
6.0時間+1.2時間+x時間=8.0時間
x=0.8時間
その他業務時間は,1.5時間-0.8時間=0.7時間削減する必要がある。
よって,ウである。
解答
ウ
基本情報技術者 平成28年度秋期 問72
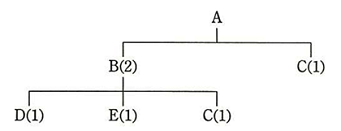
図は,製品Aの構成部品を示し,括弧内の数字は上位の製品・部品1個当たりの所要数量である。この製品Aを10個生産する場合,部品Cの発注数量は何個になるか。ここで,現在の部品Cの在庫は5個である。
| ア | 15 |
| イ | 20 |
| ウ | 25 |
| エ | 30 |
解説
「括弧内の数字は上位の製品・部品1個当たりの所要数量」である。
(イメージで解く)
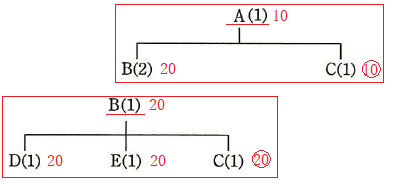
部品Cは10個+20個=30個必要であるが,在庫が5個あるので商品Cの発注数量は30個-5個=25個
よって,ウである。
解答
ウ
基本情報技術者 令和元年度秋期 問3
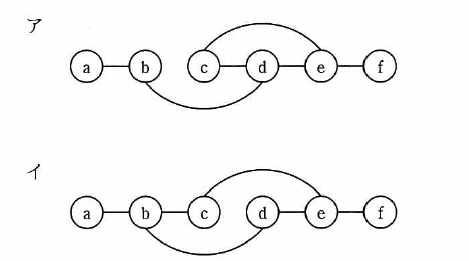
ノードとノードの間のエッジの有無を,隣接行列を用いて表す。ある無向グラフの隣接行列が次の場合,グラフで表現したものはどれか。ここで,ノードを隣接行列の行と列に対応させて,ノード間にエッジが存在する場合は1で,エッジが存在しない場合は0で示す。

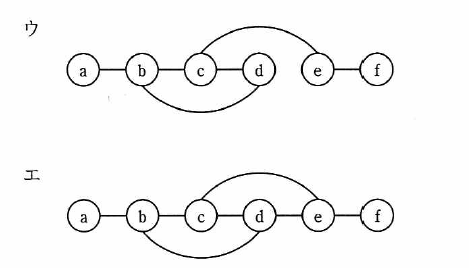
解説
(イメージで解く)
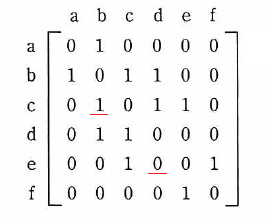
b-c:エッジ有
d-e:エッジ無
よって,ウである。
解答
ウ
