基本情報技術者講座

★　猫本　3-12　確率・統計(その2)　★

基本情報技術者　平成30年度春期　問2

図の線上を，点Pから点Rを通って，点Qに至る最短経路は何通りあるか。

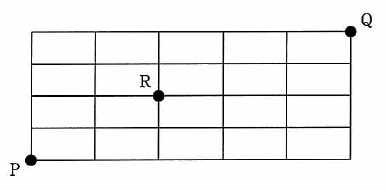
ア	16
イ	24
ウ	32
エ	60

解説

(頭の準備体操)
n個の中からr個を取り出す組合せの数は，
_nC_r＝n！/r！(n－r)！　　(n≧r)

まずは，P→R，R→Qの経路の組合せをそれぞれ求まる。

・P→Rの経路では，「上に2回」，「右に2回」移動させる必要があるため，
4回の移動のうち2回が上(残りは右)である組合せは，
₄C₂＝4！/2！2！＝(4・3・2・1)/(2・1)(2・1)＝24/4＝6通り

・R→Qの経路では，「上に2回」，「右に3回」移動させる必要があるため，
5回の移動のうち2回が上(残りは右)である組合せは，
₅C₂＝5！/2！3！＝(5・4・3・2・1)/(2・1)(3・2・1)＝120/12＝10通り

よって，P→Qの経路の組合せは，6×10＝60通りである。

解答
エ

基本情報技術者　令和元年度秋期　問4

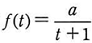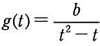a及びbを定数とする関数及びに対して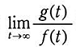，はどれか。ここで，a≠0，b≠0，t＞1とする。

解説

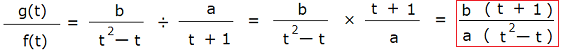
ここで，t→∞：tを限りなく大きく（∞：無限大）していくと，分母が分子よりも大きくなっていくことから，0に近づいていく。

※確率・統計分野ではありませんが，ここに掲載している。

解答
ア