基本情報技術者講座

★　猫本　3-06　論理演算(その3)　★

基本情報技術者　平成29年度春期　問3

XとYの否定論理積 X NAND Yは，NOT(X AND Y)として定義される。X OR YをNANDだけを使って表した論理式はどれか。

ア	((X NAND Y) NAND X) NAND Y
イ	(X NAND X) NAND (Y NAND Y)
ウ	(X NAND Y) NAND (X NAND Y)
エ	X NAND (Y NAND (X NAND Y))

解説

(頭の準備体操)

NAND：ANDの否定(NOT)

ア

((X NAND Y)NAND X) NAND Y

((X NAND Y) NAND X) NAND Y

((X NAND Y) NAND X) NAND Y

イ

(X NAND X)NAND (Y NAND Y)

(X NAND X) NAND (Y NAND Y)

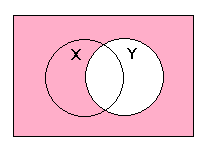
(X NAND X) NAND (Y NAND Y)

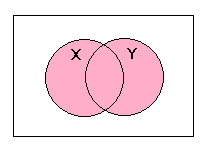
ウ

(X NAND Y) NAND (X NAND Y)

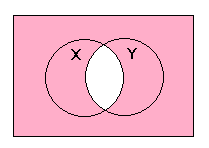
(X NAND Y) NAND (X NAND Y)

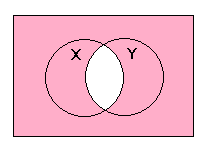
(X NAND Y) NAND (X NAND Y)

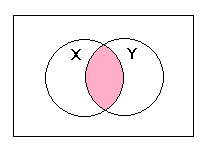
エ

X NAND (Y NAND (X NAND Y))

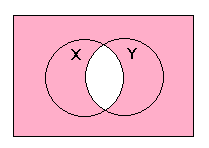
X NAND (Y NAND (X NAND Y))

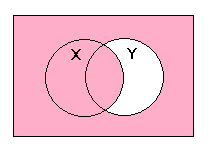
X NAND (Y NAND (X NAND Y))

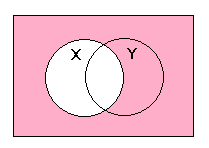
よって，イである。

解答
イ

基本情報技術者　平成29年度春期　問1

集合A，B，Cを使った等式のうち，集合A，B，Cの内容によらず常に成立する等式はどれか。ここで，∪は和集合，∩は積集合を示す。

ア	(A∪B)∩(A∩C) ＝ B∩(A∪C)
イ	(A∪B)∩C ＝ (A∪C)∩(B∪C)
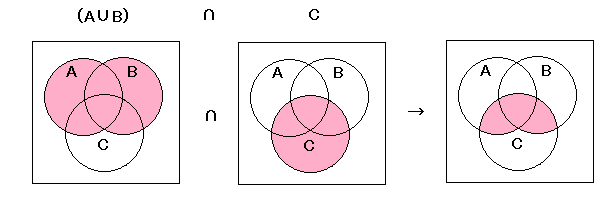
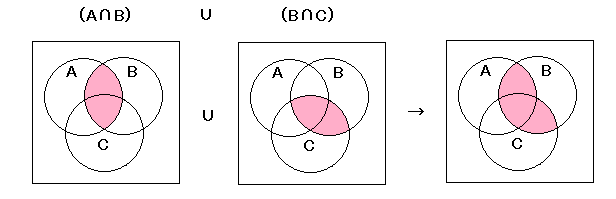
ウ	(A∩C)∪(B∩A) ＝ (A∩B)∪(B∩C)
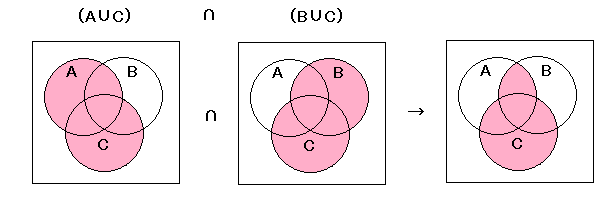
エ	(A∩C)∪(B∩C) ＝ (A∪B)∩C

解説

(頭の体操)

∪(和集合)：二つの入力の少なくとも一方が真のとき，出力が真

∩(積集合)：二つの入力がともに真のとき，出力が真

ア

左辺

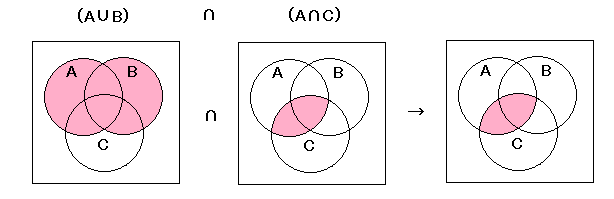
右辺

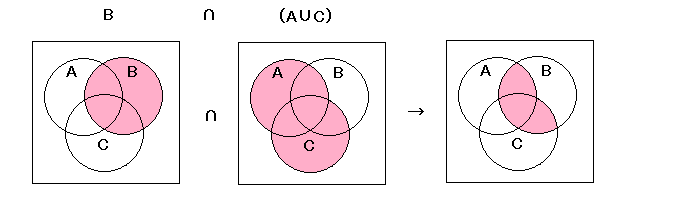
イ

左辺

右辺

ウ

左辺

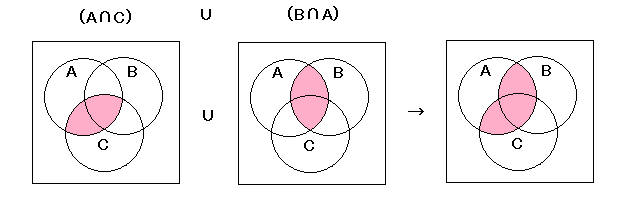
右辺

エ

左辺

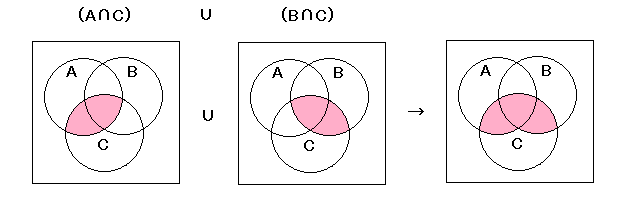
右辺

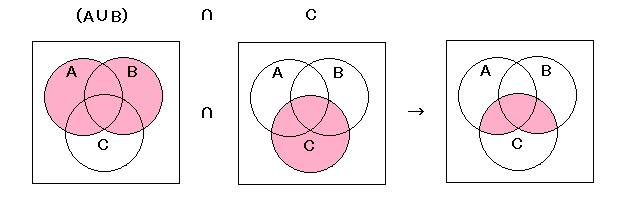
よって，エである。

解答
エ

基本情報技術者　令和4年度6月免除　問1

任意のオペランドに対するブール演算Aの結果とブール演算Bの結果が互いに否定の関係にあるとき，AはBの(又は，BはAの)相補演算であるという。排他的論理和の相補演算はどれか。

解説

(頭の準備体操)

排他的論理和：二つの入力が異なれば，出力が1

ブール演算は，論理演算のこと

排他的論理和演算

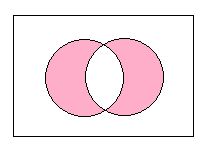
その否定の関係にあるのは，

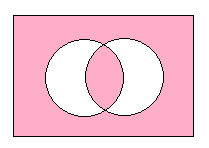
よって，アである。

解答
ア

基本情報技術者　平成31年春期　問3

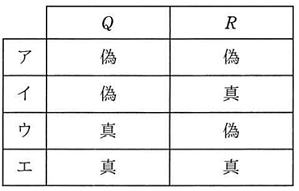
P，Q，Rはいずれも命題である。命題Pの真理値は真であり，命題 (not P) or Q 及び命題 (not Q) or R のいずれの真理値も真であることが分かっている。Q，Rの真理値はどれか。ここで，X or Y は X と Y の論理和，not X は X の否定を表す。

解説

(頭の体操)

or：二つの入力の少なくとも一方が真のとき，出力が真

「命題 (not P) or Qの真理値が真」なので，

(not P) or Q　→　真

ここで，「命題Pの真理値は真」なので，

(not 真) or Q　→　真

偽 or Q　→　真

Qは真である。

「命題 (not Q) or Rの真理値が真」なので，

(not Q) or R 　→　真

(not 真) or R 　→　真

偽 or R 　→　真

Rは真である。

よって，エである。

解答
エ